There’s a new book by French economist Thomas Piketty, called “Capital in the Twenty-First Century,” that supposedly identifies the Achilles’ Heel of the market economy.
Piketty argues that the rate of return to capital is higher than the economy-wide growth rate and that this will lead to untenable inequality as the rich grab a larger and larger share of the pie.
The solution, he claims, is confiscatory tax rates.
I’m not impressed.
Garett Jones of George Mason University has a very good review that casts doubt on Piketty’s hypothesis, but I also think Margaret Thatcher pre-debunked (if I’m allowed to make up a word) Piketty in this classic video from the House of Commons.
Simply stated, if you care about those with lower incomes, your goal should be faster growth.
If the economy is more prosperous, that means a rising tide that will lift all boats.
Piketty’s class-warfare prescription, by contrast, almost certainly will hurt the poor because of anemic growth, largely because higher tax rates will discourage productive behavior and exacerbate the tax code’s bias against saving and investment.
This means less capital and there should be no doubt about the strong link between the capital stock and worker compensation.
But I sometimes worry that this type of analysis sounds too theoretical for a lot of people and that perhaps it would be helpful to offer some tangible real-world evidence.
So it is quite fortuitous that I’m currently in Lithuania as part of the Free Market Road Showand that one of the participants is John Charalambakis, who teaches at the Patterson School of Diplomacy and International Commerce at the University of Kentucky.
In discussing the importance of economic growth, he explained that Singapore and Jamaica were economically similar in the early 1960s and then asked why they are so different today.
I have to admit that I was skeptical. I know Singapore is much richer today, but was it actually the case that it had the same level of per-capita GDP as Jamaica as recently as 50 years ago?
So I looked at the long-run data and John was exactly right. Take a look at this chart and you’ll understand why rapid growth caused by free markets is so vastly superior to the stagnation caused by statism.
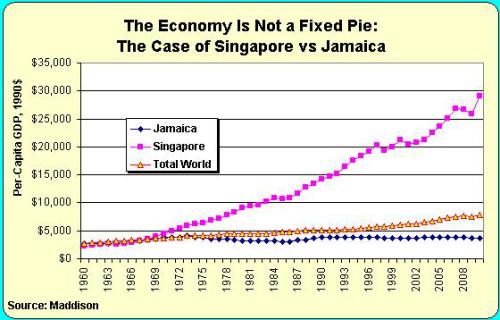
I also included the world average for per-capita GDP so you can see that Singapore easily out-paced a lot of nations, not just Jamaica.
P.S. Keith Hennessey of the Hoover Institution writes that it makes more sense to think of the economy as a garden rather than a pie.
The pie metaphor for the economy is misleading and damaging, especially if you place a high priority on economic growth. …because dividing a pie is zero-sum, the flawed metaphor assumes that if one person’s slice grows larger, it comes at the expense of others. The inapt metaphor and its accompanying flawed logic lead one to conclude that when rich people have a larger share of a bigger economy, they do so “at the expense of” others lower on the income scale. …A flower garden is a better metaphor for looking at economic growth and income distribution. A flower’s growth depends on the individual characteristics of that type of flower and that particular seed. …the rapid growth of a sunflower at one end of the garden largely does not come at the expense of a struggling tulip at the other end. The sunflower may have advantages the tulip does not, even unfair ones, but the fast-growing sunflower is not “taking growth” from the slow-growing tulip. Flowers will grow at different rates for a variety of different reasons. Policymakers should focus their energies on absolute growth rates rather than relative ones.
Keith is correct.
Or, if he isn’t correct, it’s because the garden analogy doesn’t go far enough. If my neighbor is akin to a fast-growing sunflower, that presumably creates more wealth that will benefit me and the other tulips of the world.
In other words, I’m more likely to get richer if my neighbor gets richer.
But if you like the “pie” approach, then this pizza graphic is very appropriate because it gets across the message that the pie isn’t fixed in size.

